How the polygonal masonry megalithic structures of Peru made of large stone blocks with fitted curved surfaces were fabricated?
Rostislav V. Lapshin
Kurchatov Institute, Moscow, Russian Federation
e-mail: rlapshin@gmail.com
The article suggests methods that allow creating the most complicated type of polygonal masonry found in Peru. This masonry type consists of large stone blocks weighing from several hundred kilograms to several tons fitted close to each other almost without a gap between complicated curved surfaces over a large area. The work provides a description of techniques, which apparently were used by builders who arrived from Europe. The techniques under discussion are based on the use of a reduced clay model, 3D-pantograph, topography translator and replicas. The use of a reduced clay model and a pantograph provides not only the unique appearance and high quality of masonry with large blocks, but also allows to significantly increase the productivity of the builders. As machines coping-scaling three-dimensional objects are known since the beginning of the 18th century, the stone structures under consideration should be approximately dated by this time. The remaining simpler types of polygonal masonry with smaller stones or fitted surfaces are almost flat, or stones contact with each other by a small area, or there are significant gaps between stones, are quite consistent with the well-known methods of stone processing of those and earlier years, and, therefore, they do not require any additional explanations.
Download full article (DOI: 10.20944/preprints202108.0087.v10)
Announcement. Based on the material presented here, a book “Peruvian polygonal masonry: how, who, when and what for” (R. V. Lapshin, 148 pp., Publishing Solutions, Moscow, 2025, ISBN 978-5-0067-0769-6) has been published. The book can be ordered in paper form (print on demand within 96 hours) and also downloaded in electronic form (black and white illustrations) on the Ridero. The e-book with color illustrations is distributed by the Litres platform.
Key words: stone block, polygonal masonry, clay model, pantograph, translator, parallelogram mechanism, replica, chisel, hammer, megalith, star fortress, Inca, Cusco, Ollantaytambo, Machu Picchu, Sacsayhuaman, Peru, polygonal bas-relief, polygonal Face Towers, Angkor, Cambodia, symmetrical statue, pharaoh statue, Ramses, Egypt
1. Introduction
Polygonal masonry is a type of masonry made of natural stone. Stones having an initially arbitrary shape are processed in such a way that form irregular polygons tightly adjacent to each other on the front side of the structure.1 It should be noted that the name “polygonal masonry” is largely conditional. The fact is that there are many structures classified as polygonal in which stone “polygons” have curved sections besides the linear ones. A feature of the polygonal masonry is that it does not require a building mortar (dry masonry). The polygonal masonry possesses sufficient strength and stability to withstand moderate earthquakes.2-5
In the present paper, a polygonal masonry in the megalithic structures located on the territory of modern Peru is under consideration. The main attention is paid to the masonry consisting of large stone blocks weighing from several hundred kilograms to several tons fitted close to each other almost without a gap between curved surfaces of large area. The remaining simpler types of polygonal masonry, when the stones are small6 or the mating surfaces are almost flat,6,7 or the stones contact each other over a small area,7 or there are significant gaps between the stones, are quite correspond to the long-known methods of stone processing and, therefore, do not require any special explanation.
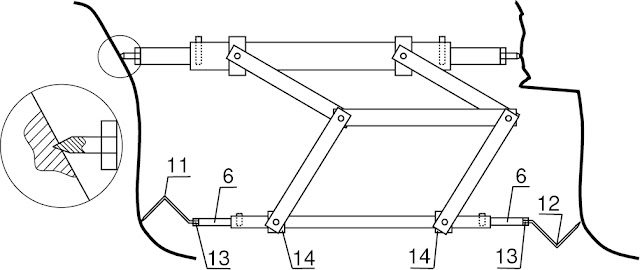
The main building materials of those years were boulders and blocks of rock of random (arbitrary) shape. As a rule, this building material did not need to be mined (broken out in quarries), since it was presented everywhere in the form of multi-meter deposits of mountain debris formed at the foot of the mountains as a result of fallings and landslides. In most cases, this material did not even need to be transported from anywhere, since construction took place usually at those locations where the material was already in great abundance. If a megalithic structure was located on top of a mountain, then the construction material was taken (broken out) here on the site. That is why, for example, the top of the mountain, where the Machu Picchu complex of buildings is located, is cut off, and the tops of the neighboring mountains, where no one lives, are sharp.
In general, a polygonal masonry is not something unprecedented, such masonry has been used in Europe since antiquity.5,8 In the Peruvian version, only the quality of the curved interfaces is striking, which is not easy to repeat even in our time. The methods suggested by both the scientific-engineering community6,9-12 and the enthusiasts13-16 for fabrication of the Peruvian polygonal masonry do not explain all the observed features and are often far from a reality.
The methods of polygonal masonry fabrication proposed by the author are based on the use of a reduced clay model and 3D-pantograph17 (see Sections 2.1, 2.6-2.10), topography translator (see Section 2.11) and replicas9 (see Sections 2.3, 2.6). The main tools for stone processing are a hammer and a steel chisel (in practice, a set of steel chisels of different types). The use of the reduced clay model and the pantograph provides not only the well-known unique appearance and high quality of masonry of large blocks, but also allows to significantly increase the productivity of the builders. Only due to the high productivity it became possible to carry out the volumes of the polygonal construction revealed in Peru for an acceptable time, engaging a reasonable amount of labor force.
If we closely look at the shape of the stones in the masonry, at the sites of their almost perfect fitting, then there is a feeling that the stones were not processed mechanically but were sculpted. In this regard, many researchers mistakenly decided that the stones were sculpted or cast from a certain plastic mixture – artificial granite, concrete, lime, rock softened by heating, and so on.13-16 In this regard, the question immediately arises: why produce an expensive plastic mixture when there is a lot of ready-to-use material around – natural stone of arbitrary shape? What is even more unclear is: why should plastic mixture be given such complex shapes? Why not make a limited range of standard concrete blocks with locking elements, for example? Nevertheless, sculpting really took place during the polygonal construction, but it was sculpting of a reduced model of the future stone block from clay, not the sculpting of the stone block itself. Further, using a pantograph, the “sculpture” was simply transferred to a stone block with the enlargement set in the pantograph by means of a hammer and chisel.
There are other arguments against the plastic version. For example, the backside of many blocks is a ragged stone; there is no plastic mixture flowed into the interblock spaces inside the masonry; the stone blocks have veinlets and other features inherent in natural stone.18 Unlike clay, concrete,13 lime, and artificial granite are not suitable for hand modeling. Therefore, the blocks cast from these materials will have flat interface surfaces, as well as flat front and back sides, determined by the flat panels of the formwork used. Thus, if, for example, smooth L- or U-shaped recesses are present in the masonry, then, most likely, this masonry was not fabricated by the casting method generally accepted in construction (see also Section 2.2).
Any products obtained by casting/sculpting16 shrink during the drying process. The shrinkage of modern concrete can reach 3%, lime shrinkage is noticeably greater. The casting shrinkage leads to casting size decrease, warping (shape distortion) and to cracking, as a result. Thus, the presence of cracks can be one of the casting hallmarks. The shrinkage-induced casting size decrease, in turn, leads to interblock gaps. Since the initial shape of the blocks in the polygonal masonry is irregular, the shrinkage in addition turns out to be non-uniform. Accordingly, the gaps resulting from such shrinkage will be non-uniform (nonparallel, see Ref. 14) too.
Thus, even if the blocks are cast sequentially one after another “by site”,13,14 waiting each time for the end of the shrinkage (ideal case), it is still not possible to completely eliminate gaps between the blocks. For the reinforcement-free concrete block with modest sizes of 50×50 cm (width×height) having typical average shrinkage coefficient of modern concrete of 1.5%, the gap between the blocks makes 7.5 mm (!). The larger are the sizes of the blocks, the greater is the value of their shrinkage, and, accordingly, the larger is the resulting gap.
Fig. 1 shows an approximate view of the cast polygonal masonry of large blocks tightly-abutted to each other. First, the large blocks are cast. After shrinkage termination, the polygonal masonry is assembled from the large blocks sequentially block by block (numbers in the figure show block installation order). Each block is installed so that it abuts closely to an adjacent previously installed block by a certain side. At the final stage, small (compensatory) spaces between the large blocks are filled with concrete (before casting, a thin layer of material is coated on the hardened concrete to prevent adhesion of the fresh concrete with the hardened one13,14). Note that the polygonal masonry obtained according to the described technology may not be completely dismountable in some cases.
It is seen from the presented procedure that the interface surfaces in the polygonal masonry obtained by casting should be close to planes and the masonry itself should have a rather specific appearance (see Fig. 1). Large non-edge blocks in such masonry are in contact with neighboring large blocks with only two of their sides, contacts of the rest sides occur through the small blocks with a small shrinkage of their own. The small blocks are designed to compensate for the shrinkage-related size reductions and shape changes of the large blocks. Only this approach allows to reduce to a minimum (but not to zero) the gaps between the concrete blocks obtained by casting.
The more sides a large concrete block has, the more the compensating inserts are required, accordingly, the more complex the formwork used is. Since there are no triangular blocks in the Peruvian polygonal masonry, the simplest shape of the block in this case is a conditional quadrilateral. The conditional quadrilateral occurs if one ignores shape changes of the large polygonal block related to inclusion of the compensation blocks in its body. Since a masonry similar to one shown in Fig. 1 was not found in Peru, the methods of casting into a formwork were not used for fabrication of the polygonal walls from large blocks tightly-abutted to each other.
In the article, besides the mechanical treatment of stones by means of a hammer and steel chisel, the method is also proposed that allows casting large polygonal blocks into a mold (see Section 2.2). In this case, the tight abutment of polygonal masonry blocks is achieved due to high casting accuracy. According to this technology, the typical signs of the casting are: a solid/hollow core made of cheap concrete-like material and a comparatively thin shell made of more expensive artificial granite.
Since at the moment of the South America conquest by Europeans, the Indians did not know neither iron tools nor a wheel, and did not have draft animals, the structures under consideration could only be erected by the builders who came from Europe (see Section 3.5). Unlike the Indians, these builders had all the necessary tools, mechanisms, and skills for the large-scale construction. The marks of this large-scale stone construction are visible everywhere – Catholic cathedrals, monasteries, palaces, villas, and a lot of urban and industrial buildings.
Any large-scale construction always implies the existence of an economy corresponding to this scale. Therefore, the article additionally explains what the economy of Peru was based on in those years (see Section 3.5). As machines coping-scaling three-dimensional objects are known since the beginning of the 18th century (see Section 3.4), the polygonal structures under consideration should be dated around this time.
2. Methods of fabrication of the polygonal masonry
2.1. Clay model shape transfer on a stone billet by means of a 3D-pantograph
First, in accordance with a sketch, the clay model of a structure is made in a reduced scale which blocks form a polygonal masonry. Let us assume for a certainty that the structure is just a wall. Small polygonal blocks of the planned shape are sculpted from clay. The sizes of these blocks correspond to the sizes, say, of a basketball or so. The surface interfaces are formed by pressing the blocks into each other. To reduce shrinkage, a solid core of suitable shape – a stone or a piece of dry clay is put inside the clay blocks.
The model of the wall is assembled from the raw model blocks. During the assembly, some material is laid between the blocks that prevents the blocks from sticking to each other during the drying-solidification process. To reduce the influence of the shrinkage effect, the bottom course is dried first, then the next course, and so on. If necessary, the wall is given the required slope (see Section 2.6). During the drying shrinkage process, the model blocks are matched more closely under their own weight and with small corrections of the builder. If a shrinkage-resulted gap appears between the model blocks, it is eliminated by putting clay layers of a suitable thickness.
After model wall solidification, it is disassembled. Now “magic” began. The Medieval European builders transferred the surface topography from a small model clay block to a large stone billet of suitable sizes and shape with a specified scale using a 3D-pantograph,17 a hammer, and a steel chisel.
The pantograph is a simple hinge-lever device based on a parallelogram mechanism.19 A 2D-pantograph allows to proportionally enlarge/reduce a flat drawing.19,20 Being a logical advancement of the 2D-pantograph, a more complicated 3D-pantograph21,22 (see Fig. 2) allows to proportionally enlarge/reduce a space figure, for example, a statue. In our case, using the 3D-pantograph, the enlarged copy of a small clay model of the block is obtained by processing the stone billet with a hammer and chisel.
 |
| Fig. 2. Modern 3D-pantograph (M. Keropian, www.keropiansculpture.com). |
The parallelogram mechanism is located on a boom of the 3D-pantograph. The boom is attached to a frame using a ball joint (Pivot in Fig. 2). The boom has a counterweight. A sharp probe is fixed on one arm of the parallelogram mechanism (Pointer A), a pointer (a part actually similar to the probe; Pointer B in Fig. 2) – on the other arm. If someone touches the clay model with the probe, the pointer will show where the corresponding point of the enlarged copy is located in the space. The enlargement coefficient is set by the appropriate adjustment of the arms of the lever system. The model and its enlarged copy are located each on their rotary platform (Table A and Table B, respectively). Due to a chain transmission, the platforms can be synchronously rotated around their vertical axes, putting different sides of the 3D-object (model/copy) under the probe/pointer.
A minimum size of the model clay block depends on the size of the stone block under fabrication and, ultimately, is determined by the error of the pantograph mechanism. The size of the model block is also determined by how convenient it is for one or two workers to handle (sculpt, correct, carry, install, shift, turn, etc.) such a block. The modern 3D-pantographs used by sculptors21,22 (see Fig. 2) allow enlargement of the object model by up to 6 times. Thus, by a clay block model size, say, 50×50×50 cm, which can be made hollow to reduce its weight and shrinkage, the stone blocks up to 3×3×3 m can be processed on the not very large pantograph.
 |
| Photo. 1. Cusco (V. M. Soroka, 2021). |
It should be noted that by installing a stone billet on the pantograph, the clay model of the block suitable for this billet can be quickly selected. This feature is extremely useful exactly in the case of the polygonal type of masonry, since in such masonry, initial stone blocks often have a complicated shape that requires a lot of preliminary measurements while selecting a billet.
After the mentioned copying process with the specified scale, the wall of stone blocks is assembled without any adjustments using rollers, levers, steel crowbars, blocks, winches, and cranes of the time.11,12 The front side of a stone block can be copied from the front side of its clay model, but it can be dressed or refined after the polygonal structure assembly.
When a polygonal masonry is built on a leveled reinforced ground, the first course is formed of not large stone blocks having a flat base, which are processed by the corresponding clay models. The stone blocks of the second course are usually noticeably larger than the blocks of the first course (see Photos. 1-5, for example). Why is that? Why are the large blocks of the second course not put on the equally large or even larger blocks? There should be good reasons for such a masonry arrangement. Indeed, the higher a large heavy block is located, the higher is its gravity center, the less stable is the wall. Moreover, the load bearing capacity of small stones is less than that of large ones.
As an example, let us consider the wall on the Hatunrumiyoc street in Cusco (see Photos. 1-5). Since the street has a slope, one might think that the small stones in the base of the large blocks of the wall are needed to account for this slope. However, there are sections of the polygonal masonry in this wall, where one course of stones splits into two or two courses merge into one. For example, in Photo. 1, moving from left to right, the second and the third courses merge into single course – the second course; and the fourth course splits into two courses – the third and the fourth. Thus, we see that the street slope could always be taken into account using the technique of masonry course merging/splitting.
 |
| Photo. 2. Cusco (V. M. Soroka, 2021). |
In fact, everything is simple. Only by adding the soil under the not large blocks of the first course and putting small stones as wedges under them, it is possible to take up the side gaps between the large stone blocks of the second course, i. e., correctly locate these blocks relative to each other. Only provided that the relative position of the large blocks is correct, the rest above located courses can be laid with minimal gaps.
This peculiarity is one more confirmation that the wall of polygonal blocks of the type under consideration was not built course after course with fitting the stones “by site”,10 but it was fabricated by a reduced clay model and then it was only assembled. During the course-after-course construction, the first course of the masonry would always consist of the largest stone blocks, since according to this approach, both the mounting surface for the next stone block and this stone block itself are successively made by site.
If the base of the not large stone blocks of the first course stands out of the general aesthetics of a particular polygonal masonry, then it can be hidden by a layer of soil (see Photos. 5, 10). The soil being added will be compacted and the inserted small stones-wedges can crack and crumble under the masonry weight, then the masonry will slide apart. To prevent such event, solid wedging stones having no visible defects should be used and not in one but in several places; the soil under the building should be strengthened;10 after laying the first two courses, the work on this site should be stopped and the masonry should be observed for some time, etc.
When a polygonal masonry is located on a bedrock, the bedrock is pre-prepared. For example, L- or U-shaped recesses are fabricated in the bedrock. Then, not large model blocks of the first course are formed from clay on the prepared section of the rock, which are made hollow to reduce their weight and shrinkage. After drying, the full-sized clay blocks are removed from the bedrock and put in the pantograph in place of a stone billet (Table B in Fig. 2). Using the pantograph, reduced clay models are fabricated by the full-sized clay blocks of the first course. The obtained reduced models of the first course are dried.
 |
| Photo. 3. Cusco (S. N. Kozintsev, photo.sirano.info). |
To avoid lower surface damage of the model blocks of the first course, the model blocks are put in beds with a flat base by pressing into raw clay bars. The correct mutual position of the model blocks of the first course is determined by abutment of these blocks to each other along the side faces. To reduce the error of the relative position, one should aim to make the areas of the side faces of the first course blocks comparable to the areas of the bases of these blocks. The correct mutual position of the first course blocks at the model wall construction site is carried out by adding soil and putting small wedging stones under the beds of these blocks.
The proposed method of geometry transfer from a small clay model to a large stone block using a 3D-pantograph does not require the detailed drawing of the block geometry. The builder should actually sculpt approximately the block and its interface with the neighboring blocks in accordance to a general idea of the sketch with his own hands (and applying tools such as spatulas, straighteners, scrapers, wire loops, and the like); then lay this block in the model wall, where it would be finally fitted to the neighboring model blocks under its own weight and with small corrections of the builder. No precise dimensions need to be held here.
2.2. Pantograph application for fabrication of the polygonal masonry blocks by casting
Using the proposed method, it is also possible to obtain large blocks of concrete, lime, artificial granite and other materials by casting them into a mold. Using the pantograph, the reduced clay model of a block is enlarged to the desired size. The enlarged clay model is made hollow to reduce weight and shrinkage. Next, a mold is fabricated by the enlarged clay model.
 |
| Photo. 4. Cusco (V. M. Soroka, 2021). |
Since shrinkage has a significant effect on the value of the interblock gap, the cast blocks can be made hollow to reduce it. Moreover, the cast blocks can be made of two components – a core (solid or hollow) of cheap concrete and a comparatively thin outer shell (“plaster” layer) of more expensive artificial granite. First, the core is cast. Then, after the end of the shrinkage, a fairly thin shell is cast over the core. Shrinkage of the shell is insignificant due to its small thickness. To ensure the strength and durability of the shell, its coefficient of thermal expansion (CTE)23 should be as close as possible to the CTE of the concrete core.24
The enlarged clay models for hollow/solid core and for the outer shell are fabricated by the same reduced clay model of the block using a pantograph set to the appropriate enlargement factor. To increase adhesion of the shell to the core, radial grooves are created on the front and side surfaces of the enlarged core model. The grooves are created either directly by the pantograph pointer (Pointer B), or by a wire loop attached to the pointer. Despite exfoliations on the granite blocks of some Peruvian structures that are similar to the described outer shell (see Photos. 1-3, 5 and 15), the thicknesses of these exfoliations are small and thus these exfoliations should rather be attributed to the results of natural stone destruction or unsuccessful restoration/conservation.
Although the proposed casting method is able to provide the polygonal masonry fabrication from large blocks tightly-abutted to each other, it is much more laborious in comparison with the mechanical processing method. The fact is that, besides the reduced model, this casting method requires additional fabrication of two more clay full-sized models of the block at least, followed by fabrication of two molds by these models – one for the concrete core, the other for the shell of artificial granite.
 |
| Photo. 5. Cusco (V. M. Soroka, 2021). |
The method can be simplified and made cheaper using a roughly mechanically processed natural stone as the core, which shape approximately repeats the shape of the final product in a reduced scale. However, in this case, the shell will likely have an unequal thickness, which, in turn, may affect the constancy of the gaps between the blocks. The required stone block acting as a core can be fabricated either simply by basic dimensions or by the reduced clay model using the pantograph. In the method under consideration, the backside of the cast block may not have an outer shell layer at all since in most buildings, taking up a gap between the blocks or taking care of the product appearance is not necessary at this location.
Since stone blocks in a polygonal masonry experience a weight load from several tons to several tens of tons, under certain circumstances, say, during tremors caused by an earthquake, the destruction of the outer hard but fragile shell of artificial granite may occur. The listed features show that although the presented casting method is capable to provide the desired result (small gaps), it is too complex and expensive for construction purposes, and it does not guarantee the necessary structure durability in the earthquake-prone region.
2.3. Usage of replicas
Not very complicated interfaces between large blocks are fabricated using replicas. A “pancake” of a constant thickness is pressed/rolled out of the clay. The raw pancake is put on a stone block which surface replica should be made. After solidification, the replica-pancake is taken off. By periodically applying the obtained low weight replica-pancake to a heavy mating stone block, the excess material is gradually removed in the needed areas until full fitting of the replica to the block.
If a higher accuracy of the relief transfer is required than the replica-pancake is capable to provide, then a replica of the replica is produced. First, by applying a raw clay bar to the selected area of the stone block, an imprint of its surface is made. After solidification, another imprint is made in raw clay by the obtained replica. After drying, the replica of the replica is further used as a copy of the surface area of the stone block when making the mating part of the stone masonry.
 |
| Photo. 6. Ollantaytambo (C. Jansen, M. Düerkop, 2016, www.travel-badger.com). |
In another method, a clay rim is installed along the perimeter of the selected area of the stone block, after that the formed container is filled with gypsum. After solidification, the obtained replica is imprinted in a raw clay or, having installed a rim, one fill the formed container with gypsum (the surface of the gypsum mold is precovered with a substance preventing bonding of the poured gypsum to the gypsum mold). After drying, the resulting replica of the replica is further used as a copy of the surface area of the stone block when making the mating part of the stone masonry.
The replicas were also used in the sites where the stone structures of large blocks were abutted upon rocks. The replica was taken from a pre-prepared rock section and then applied to the processing stone block or, vice versa, the replica was taken from a processed stone block and then applied to the processing rock. It all depended on what was more convenient in each particular case. Since very large stone blocks are like rocks – they being extremely difficult to move, the replicas were also used for joining large blocks to very large blocks and very large blocks to other very large blocks.
The larger are the sizes of a stone block, the larger and heavier are the replicas fabricated by it. Therefore, beginning from a certain size of the stone block, replicas have to be taken from sections of the stone block. To ensure the correct mutual position of the replicas on the processed mating surface of the block/rock, the sections of the neighboring replicas should be partially overlapped.
The disadvantages of the replicas are: a higher interface error of adjacent blocks in comparison with the pantograph and a higher fabrication laboriousness in comparison with the reduced block model. The replica error is mainly caused by a clay/gypsum shrinkage. The shrinkage-related error of the replica replica is twice that of a single replica. To reduce the shrinkage-caused error of the replica replica, a thin layer of raw clay is applied to the replica; after that the replica is pressed against the original. As a result, raw clay fills the voids, after that the replica and the original are separated, then the replica is dried. Next, the similar operations are performed with the replica replica. If necessary, the process is repeated.
 |
| Photo. 7. Ollantaytambo (B. Everett, www.facebook.com/barry.everett.3). |
The advantage of the replica is that just one of the mating surfaces of the adjacent blocks is processed upon a model (replica); the original surface is processed arbitrarily (independently). In contrast to the replica, it is necessary to process both mating surfaces by the model in the pantograph method. There are no arbitrarily processed surfaces in the pantograph method.
2.4. The main problem
What does a stonemason has to continuously do while fabricating blocks fitted to each other through a complicated profile? The stonemason has to repeatedly apply one stone to another in order to determine the areas where the excess material should be removed. When the stones are small, it is easy to do.6 But how to do this when the weight of the stones is hundreds of kilograms or several tons? The suggested methods just allow us to solve this problem. It is no longer necessary to repeatedly move a heavy mating block.
 |
| Photo. 8. Ollantaytambo (C. Boudou, 2013). |
2.5. What else was the clay model of the object needed for?
It is always extremely useful:
- to have a small model of the object consisting of many parts of a complicated shape connected to each other in a complicated way;
- to turn each block in hands;
- to evaluate proportions more precisely;
- to correct the blocks if something is disliked in their shape or fitting;
- to assemble/disassemble the model wall to check the fundamental possibility of assembling the object containing locking elements;
- to assemble/disassemble the model wall to analyze the operations for moving, mounting, and installing heavy stone blocks;
- to see in advance how the object will look after the end of construction.
In those days, architects and builders had no computers to rotate a component in three-dimensional space on a monitor screen or, creating a virtual reality, wander around the future construction long before its erection. Even in our time, the making of scale models in architecture and planning did not lose its relevance.
It is well-known that the region, where the polygonal masonry was used, is earthquake-prone.2-5 Therefore, by creating a model of the building with lock blocks and shaking it, one could see how the object would behave in an earthquake, after that make appropriate corrections to the project, if necessary. Other methods did not simply exist in those times, calculations were rough, and the intuition and experience could fail.
As shown above, both the concrete castings and the clay models have a shrinkage. Consequently, the shrinkage-caused gaps should occur between the blocks of the polygonal masonry in both cases. Then what is the advantage of the clay model? The fact is that if the shrinkage-caused gaps occur in the clay model of the wall, these gaps can always be repaired by putting a thin clay layers on the clay model blocks where needed. In this case, any requirements related to the strength and durability of the added clay layers are simply not applicable, since the clay model is just an auxiliary element of the construction process not experiencing heavy loads, which is thrown away after a short use.
 |
| Photo. 9. Ollantaytambo (B. Foerster, 2009, hiddenincatours.com). |
But it is useless to cover a concrete casting with a thin concrete layer of several millimeters thick, since the adhesion of this layer with the casting will not be strong enough and this layer will fall off or fail very soon under weight load and weather conditions. A thicker layer can be applied to the concrete casting covering the entire casting surface rather than a separate region (see Section 2.2). This layer will adhere better, but the construction technology for such layer formation is too complicated and expensive.
Thus, the signs of a recent construction (casting) and/or unsuccessful restoration (Fortress Sacsayhuaman, complex Tarawasi) are: cracks in blocks, traces of concrete mortar application, layered structure of disintegrated blocks (“melted” stone), large gaps between blocks and non-parallelism of these gaps, falling apart polygonal masonry, failure to completely demount the masonry.
On the upper faces of a number of demounted stone blocks in Ollantaytambo, characteristic L- and U-shaped recesses for the bases of the blocks installed over draw attention.6,10 Some of these recesses spread over two or even three adjacent blocks thereby providing bonding of the blocks. According to the rules of stable equilibrium, the recesses ensure that the blocks would return to their initial position in the event of a small earthquake-caused horizontal displacement (along the wall). The recesses under consideration in the upper faces of the blocks and the corresponding protruding parts at the lower faces of the blocks installing over are fabricated while sculpturing the clay model.
Since the clay model of the wall is building bottom-up and drying course after course, then, in theory, the shallow depressions should naturally occur in the bases of the model blocks, which, being softer (wet), weigh down on the harder (dry) blocks located under them. The materials available to date do not allow us to confirm or disprove the presence of such depressions with certainty.
 |
| Photo. 10. Temple of Ten Niches, Ollantaytambo (P. Adams, 2012, manboyinthepromisedlanddotcom.wordpress.com). |
2.6. What are the advantages of the pantograph over a replica?
When we apply a replica to a processing extensive surface of complicated topography, we do not clearly see where and how much material should be removed. Therefore, when using the replica, we should stain it by something, say, chalk or charcoal, and, applying it to the processing surface area, slightly rub it to mark the locations, where stone material should be removed. Remember, what a dentist does after filling the tooth. He puts a piece of carbon paper on the filling and asks to close your mouth and slightly rub it with teeth. After that, the dentist removes a little bit of the filling material in the marked place. Then he repeats the process several times until the teeth when closing would take the correct position.
When working with the pantograph, the sharp probe (Pointer A) is applied to the clay model, and the pointer (Pointer B), which is mechanically connected to the probe by means of the parallelogram mechanism, is applied to the processing surface of a billet. In contrast to the replica, due to the small area of the probe and pointer, the topography measurement is actually carried out in a surface point, and it is clearly visible in what exact point; the entire surface is completely open.
Moreover, the pantograph allows one to clearly determine the thickness of the material to be removed at any point to which the pointer is directed (see also Section 2.11.2). Therefore, the excess material can be removed for significantly fewer attempts. All these result in increasing productivity abruptly. The highest productivity is achieved when two people work with the pantograph. One person by the pantograph pointer shows a location (point) on the stone billet and reports the thickness of material that should be removed at this point, and the other person with the hammer and chisel removes the specified amount of the material.
Another advantage of the pantograph in comparison with the replica is that it is much faster and easier to touch the clay model of the block with the almost weightless probe (the device is balanced by a counterweight) than to apply the relatively heavy replica to the stone billet, and then in addition to slightly rub with this replica by the billet.
Also, the pantograph allows to easily keep proportions set by an architect, that, in case of the replicas, have to be done by eye by spending a long time selecting billets of suitable sizes. Imagine that you need to accurately fit a structure into some unchangeable or difficult-to-change dimensions, say, between two rocky outcrops or into a cave. To do this, it is enough to measure the distance between the rocky outcrops, the size of the model, divide first by second and set the obtained enlargement factor in the pantograph.
 |
| Photo. 11. Temple of Ten Niches, Ollantaytambo (A. Fuchs, 2008, sy-akka.de/wordpress). Pay attention to the symmetrical arrangement of the blocks in the masonry. |
What else does the use of the clay model blocks and the pantograph give? Let it be required to make the outer side of the wall with a slope. To do this, it is sufficient to lay the raw clay model of the wall on the back side, install the stops setting the required slope, put a flat panel on top of the front side, and allocate above suitable weights. Instead of the weights, tightening clamps can be used. After some time, the clay model of the wall will be deformed properly. In the method, the specified angle can be kept very accurately along the whole length of the wall.
2.7. Reverse approach: clay model creation by a stone billet, formation of the interface surface and its transfer on the stone billet
According to the method described above, first, a clay model was created by a sketch, and then the stone billet was selected for each block of the model. This approach allows us to repeat many times a section of the wall (if necessary, at different scales) using the same clay model each time (see a probable example of such masonry in Ref. 25). The drawback of the method is the large volume of the chipped off material of the stone billet. The analysis shows that a reverse method was mainly used for the polygonal masonry.
In the reverse method, first, a reduced clay model is created by a stone billet of arbitrary shape using the 3D-pantograph. To do this, a piece of raw clay is impaled on a pointed, say, three- or four-sided metal pin located in the center of the rotating platform intended for a model (Table A in Fig. 2). Due to this pin, the model can be removed from the pantograph at any time and precisely returned to its original position.
Clay is added to those places of the model where it is not enough. Removal of clay excess is carried out directly with the metal pointer (Pointer A in Fig. 2; instead of a tip, a suitable tool can be attached to the pointer, for example, a wire loop, cutter, scraper, etc.) of the pantograph, which probe (Pointer B) moves along the surface of the stone block vertically up, then a small turn of the platform with the billet (Table B) around the vertical axis, then down, again a small turn, again up, etc.21 Owing to the pantograph, creation of the clay model body by the stone billet does not take much time.
At the next stage, a prototype of the wall is assembled from the obtained clay model blocks. The blocks still have no specially prepared mounting surfaces. Taking into account the sizes and the shape of the blocks, each block location is defined in the wall prototype. An architect-builder approximately layouts the contours of the future interfaces on the clay model of the wall, which should reflect: a conceived style, ensure stability of the created polygonal masonry, and minimize the labor of processing of the mounting surfaces. Further on, according to the accepted layout, the clay is cut out in the model block regions by which the blocks will adjoin each other.
Next, the wall model is being assembled from the obtained model blocks. By small corrections, the blocks are matched more precisely to each other. If the block model was occasionally damaged during the manipulations, the shape of the model in any location can always be restored by placing the block model back on the pantograph (on the above indicated pin) and by comparing with the shape of the original stone billet. Then the wall is being dried. First, the bottom course is dried, then the next one, and so on. During the drying shrinkage process, the model blocks are matched more closely under their own weight and with small corrections of the builder. If a shrinkage-resulted gap appears between the model blocks, it is eliminated by putting clay layers of the corresponding thicknesses on the model blocks at their interface.
At the final stage, the model wall is being disassembled. The clay model of the block is put back on the pantograph (on the above indicated pin) and the mounting sites are transferred on the stone billet corresponding to this model block using the hammer and chisel.
In the described method, the stone block is installed in the pantograph at least twice. To accurately return the stone block to its initial position, two lines radially diverging from the center of the platform (Table B) can be plotted on the platform. At the first installation of the stone block, alignment marks are applied to the surface of the stone with paint in the places where the lines come out from under the block.
2.8. Several more advantages of the pantograph
The use of the reduced clay model and pantograph allows block fabrication directly in the quarry where the stones are extracted.6,10 As a result, the finished stone blocks are carried from the quarry to the construction site. This approach significantly reduces the weight of the transported blocks and overall cargo traffic. Moreover, such organization excludes a large amount of construction debris on the construction site, which needs to be also transported somewhere after all.
Both the pantograph method and the replica method use auxiliary elements. In the pantograph method, these are the clay model blocks; in the replica method, these are the replicas themselves. To mate stone blocks in the replica method, the side surface of the block must be divided into several overlapping sections, each of which requires its own replica. If you mentally attach to the side surface of a non-edge stone block all the replicas made for it and by it, you will get a kind of a wheel, i. e., a fairly massive formation. If a replica of replica is used, then there will be two such “wheels” already. Thus, it is necessary to fabricate one “wheel” of replicas for each non-edge block in the replica of replica method. Let us compare such a “wheel” of replicas with the small model blocks in the pantograph-based method. The advantages of the pantograph are obvious.
2.9. Method combining elements of the replica, clay model, and pantograph methods
In the beginning, every second stone block of the first course is installed on the site of the future structure (see Fig. 3). The empty positions between these blocks will be occupied by stone blocks, which will be fitted “by site” to these initially installed blocks at the next stage using a full-sized clay model and the 3D-pantograph. The heights of the stone blocks installed between the initial blocks should be approximately two times the heights of the initial blocks. The base surfaces of the initially installed stone blocks are pre-treated properly to ensure their stability.
Besides the prepared base, the initially installed blocks have finally processed side faces also. Processing of the side faces is straightening of a complicated initial shape of the stone billet by surfaces close to the planes with the hammer and chisel. The slopes of the side faces of the initially installed blocks to the bases of these blocks should not exceed 90°, if possible, in order to facilitate the subsequent installation of the adjacent blocks. The similar rule is applied later for every second block of the subsequent courses of the polygonal masonry.
 |
| Photo. 12. Ollantaytambo (B. Everett, www.facebook.com/barry.everett.3). |
Next, the space between the initially installed blocks is filled with clay. Actually, clay models of the blocks are created at the scale 1:1 in the spaces between the initial blocks. The side surfaces of these models contacting at the left and at the right with the side surfaces of the initial blocks are, in fact, their replicas. To decrease weight of the full-sized clay models and reduce their shrinkage deformations during drying, the models are made hollow. If a shrinkage-resulted gap appears between the initial stone block and the clay model, it is eliminated by putting a corresponding thickness raw clay layer on the clay model.
After drying, the clay model of the block is removed from the structure and installed in the pantograph in the model place (Table A). The corresponding stone billet is installed in the copy place (Table B). The pantograph is adjusted to the scale 1:1 (at the given scale, the placement of the model and the copy in the pantograph is only determined by operation convenience). If necessary, one can quickly check the matching of the selected stone billet to the model with the pantograph.
Next, the interface surfaces are transferred from the full-sized clay model to the stone billet using the pantograph, hammer and chisel, as described above. After transferring the interface surfaces, the rest (arbitrary) faces are formed on the remaining side surface of the stone billet. Processing of these faces is straightening of the complicated initial shape of the stone billet by surfaces close to the planes. Further, these faces will no longer be processed. The stone block obtained this way is finally put in its position in the polygonal masonry.
Having finished the first course, the next one is produced in the same way. As in the above methods, the stone blocks of an arbitrary shape are used in the described method. The method provides good vertical bonding of the blocks. Since the method has no a full-fledged clay model of the structure, to put together the original stone blocks well and thereby minimize the amount of material to be chipped off during processing, it is desirable to preliminarily lay out the stone blocks on the ground with the backside down, one next to the other.
 |
| Photo. 13. Ollantaytambo (I. Otkalo, 2015, peru-info.me). |
The method disadvantage is the high laboriousness associated with the fabrication of the clay model of the block in the scale 1:1. Nevertheless, in comparison with the replica-replica method, this method is capable to provide a much higher accuracy of the interface between the contacting surfaces when it is necessary. As in the replica cases, about half of the side surface of the stone blocks is processed arbitrarily in this method.
The Wall of Six Monoliths at Ollantaytambo (see Photo. 14) consisting of one conditional course was most likely constructed according to the described method. Leaving aside the architectural appearance of the monument for a while, let us ask the question: why are the monoliths not connected to each other directly, but require intermediate inserts? The fact is that the use of replicas on such extended contact areas of the side surfaces of the monoliths is unable to provide a zero gap. Therefore, the intermediate inserts were needed to connect the monoliths.
To emphasize the gigantic dimensions of the monoliths, the inserts should significantly differ from the monoliths in width. Since fabrication and installation of a single narrow monolith-high insert is even more difficult technical task than the direct fitting of the neighboring monoliths, the intermediate inserts were divided into 3-5 separate parts. Each insert was fabricated by site and installed sequentially one after another – first, a row (conditional) of the lowest inserts, then the next row of inserts, etc. During wall assembly, some of the intermediate inserts were lowered on their place from top to bottom, some were installed from the front or back side of the wall.
One should pay attention to the small stones on which the monoliths rest. These stones ensure taking up the side gaps between the monoliths and the lowest narrow vertical inserts (see Section 2.1). However, the considered method of block joining does not need such position adjustment, since fabrication of the intermediate inserts here is carried out by site. It follows that the Wall of Six Monoliths was once reassembled. The need for reassembly could arise due to errors in the basement preparation of the monument or in connection with a falling apart blocks due to an earthquake, etc. Apparently, at the final construction stage, the small stones in the base of the reassembled monument were supposed to be hidden by a floor level.
 |
| Photo. 14. Wall of Six Monoliths, Ollantaytambo (P. Špindler, 2008, commons.wikimedia.org). |
2.10. “Planetary” pantograph for use in construction
The modern 3D-pantographs used by sculptors have two synchronously rotating platforms. A model is installed on one platform (see Table A in Fig. 2), and the enlarged copy of the model is installed on the other platform (Table B). Usually the enlarged copy is hollow, so the weight of the copy is not high, as a rule. The reinforced platform of such pantograph applied for construction purposes is able to withstand stone billets weighing up to 700 kg. When a sculpture is large and heavy, its model can be divided into several parts. An enlarged copy can be fabricated for each such part; then a large sculpture is assembled from the obtained enlarged copies (apparently, the polygonal Face Towers of the Cambodian temple complex Angkor26 were made using this technology). However, this is not our case.
The modern 3D-pantograph is not suitable for working with large and heavy billets. Instead of the existing design, one can offer the following “planetary” pantograph. The heavy billet in such pantograph is simply installed on a plane site and the frame, to which the pantograph boom and the platform with the model are attached, is turning during work in the horizontal plane around the stationary standing billet. As the frame turns, the model also turns around its vertical axis at the required angle (actually retains its original orientation in the space) using an appropriate mechanism. One revolution of the support point (Pivot in Fig. 2) of the pantograph boom around the billet corresponds to one revolution of the model around its axis.
Since, unlike a sculpture of, say, a human, stone blocks of a polygonal masonry have a fairly simple shape (in particular, the masonry blocks do not contain undercuts), the planetary constructional 3D-pantograph can be simplified by excluding the parallelogram from its design. In this case, the pantograph probe and pointer are attached directly to the pantograph boom perpendicular to it (as an example, see the pantograph design by J. Watt discussed in Section 3.4).
In contrast to the existing pantograph, the planetary pantograph occupies more space, and the person using the pantograph has to move while working along with the turning frame around the billet. These features can be attributed to the shortcomings of the planetary pantograph, which, however, are not critical at all in the construction field.
2.11. Topography translator based on the double parallelogram mechanism
One can suggest a plain mechanical device – a topography translator (see Fig. 4), which, in the case of a relatively simple polygonal masonry, allows to perform quite acceptable joining of the surfaces of adjacent stone blocks “by site”. To process with this device, both mating stone blocks are put on the ground on their backsides. Thus, the base, the top side, and the lateral sides to be processed would be arranged vertically in this method.
 |
| Photo. 15. Ollantaytambo (E. Berzin, 2020, allenatore.livejournal.com). |
First, the mating area of the surface of the first block is subjected to an arbitrary processing. During the processing, the surface in this area is made smoothly changing, close to a plane. Such a surface is obtained when a stonemason makes a flat surface manually “by eye” controlling no deviation of the treated surface from the plane in any way.
Then, near the first block, a second stone block is put. The second stone block is located so that the surface areas under fitting are opposite each other. The distance between the blocks is set such (60-80 cm) that a stonemason could accommodate between the blocks and would be able to work with a hammer and chisel in the space between these blocks without much trouble. Next, the proposed topography translator is installed between the blocks as a strut, so the stonemason can use it to transfer the inversed topography of the previously processed surface area of the first block to the second block.
In general, the lateral surface of a stone block is a set of the mentioned conditionally plane surface sections. The conditionally plane sections can adjoin each other forming a sharp boundary or they can pass into each other smoothly, for example, as in the L-shaped recesses. The U-shaped recesses are reduced to a pair of counter-located L-shaped recesses. Let us further describe in more detail the translator and the stone block processing sequence built on its application.
2.11.1. Topography translator design
The topography translator consists of two parallel rods connected to each other by means of the double parallelogram mechanism (see Fig. 4). The double parallelogram mechanism belongs to the hinge-lever guiding mechanisms, has two degrees of freedom and consists of seven links such that AB=A'B'=BC=B'C' and AA'=BB'=CC'.19 In the translator under consideration, the rod bodies are part of the double parallelogram mechanism. The rod with a bigger cross-section will be called a carrying rod; the rod with a smaller cross-section will be called a measuring one. Due to a telescopic or other jointing, the lengths of the rods can be coarsely changed by sliding in and out the edge sections along the rod. After the end of the rough adjustment of the rod lengths, the relative positions of the edge sections are fixed with pins.
Tip-supports are screwed into the ends of the carrying rod, which unscrewing securely fixes the translator rod like a strut on the processed area between the mating stone blocks. Pointed tips are screwed into the both ends of the measuring rod. The pointed tip directed to the pre-treated surface of the first block will be called a probe; and the pointed tip directed to the processing surface of the second block will be called a pointer. By screwing in/out the threaded pointed tips, the length of the measuring rod is set precisely. The set positions of the supports and the pointed tips are fixed with lock-nuts.
 |
| Fig. 4. Continuation. |
If the carrying rod is installed as a strut between the blocks perpendicular to the mating surfaces, then the flat foot supports are used (see Fig. 4(a)). If the carrying rod is installed as a strut with a significant inclination to the mating surfaces, then the pointed supports are used (see Fig. 4(b)). In the latter case, before installing the carrying rod, small recesses are made in the stones at the installation locations of the supports. The recesses are necessary to prevent slipping of the supports of the carrying rod.
Since the translator must transfer the spatial topography of the surface, and the double parallelogram mechanism has only two degrees of freedom, the parallelogram mechanism is attached to the carrying rod through cylindrical hinges. Thus, due to the cylindrical hinges of the carrying rod, the measuring rod together with the double parallelogram mechanism can freely rotate around the carrying rod. Such rotation makes it possible to “readout” the transferred topography by the probe of the measuring rod around the installation position of the carrying rod.
2.11.2. Outlines of operation with the topography translator
If the carrying rod of the translator is installed near the location of the longest distance between the blocks, then the longest distance is set in the measuring rod by site, and the topography transferring starts from this location. Generally, the carrying rod can be installed in any location convenient for the stonemason. In practice, it is often convenient to install the carrying rod closer to the block edge, and to begin topography transfer (translation) from the block edge.
After installing the carrying rod and setting the necessary length of the measuring rod, the probe tip of the measuring rod is applied to the pre-treated surface of the first stone block (shown in the figure on the left). As a result, the pointer tip of the measuring rod will show the point on the counter processing surface of the second block (shown in the figure on the right), where the stonemason should chip off material.
If one made the translator pointer sinkable into the retractable section of the measuring rod, spring-loaded, equipped with a scale and a mark (these elements are not shown in the figure) then a stonemason will know how much material should be chipped off in this point. The similar pointer device can also be used in the design of the 3D-pantograph. Thus, having information about the amount of material to be removed at each surface point, the stonemason performs the work in fewer chippings significantly improving his productivity.
The highest productivity is achieved when two people operate with the translator. One person with the translator pointer shows a location (point) on the stone block under processing and says the thickness of material that should be removed at this point, and the other person using the hammer and chisel removes the specified amount of the material.
The main purpose of the double parallelogram mechanism is to ensure strict parallelism of the movement of the measuring rod. It can be seen from the above description that the translator under consideration provides on a separate mating section the same result as the 3D-pantograph adjusted to the scale 1:1.
Translator accuracy is determined by gaps in the hinges and by bending deformations of the structural elements of the mechanism. To ensure structure rigidity, the bars and hinges used in the parallelograms have the appropriate cross-section sizes and stiffeners (not shown in the figure). To increase structure rigidity, besides the mentioned parallelogram mechanisms, additional identical parallelogram mechanisms can be used by attaching them both in parallel and in series (along the rods).
The translator mechanism has a limited movement space, which is a cylinder of 2AB radius (the axis of the cylinder is the carrying rod). Therefore, when operating with large blocks, it is impossible to process the entire mating surface in one installation of the translator. Moreover, due to the finite dimensions of the parallelogram bars, hinges and rods themselves, the area in the immediate vicinity around the installation location of the carrying rod and at this very spot also turns out to be unreachable for processing. (see Fig. 4).
Thus, after processing the area of the mating surface reachable by the measuring rod, the position of the measuring rod is fixed at the edge of the processed area like a strut by slightly unscrewing the probe and/or the pointer from the rod (sinkable pointer is blocked by a special pin). If the measuring rod is light enough and the hinges of the double parallelogram are not tight then the measuring rod fixation can be performed by compressing the spring of the sinkable pointer on the still unprocessed area of the stone block. After that, the carrying rod is released and transferred parallel to the fixed-in-space measuring rod at a new position, where it is again fixed as a strut. Finally, the measuring rod is unfixed, and the work continues on a new area of the stone block adjacent to the previous one.
To avoid an upset of the specified length of the measuring rod and a blunting of its probe and pointer when installing the measuring rod as a strut, it is possible, after moving the measuring rod to the edge of the translator's travel range, to simply mark with a paint the point that the probe touches and the point that the pointer looks at. After that, the carrying rod can be unfixed, moved and installed by supports on the paint-marked points. Note that, having a number of such marks and using the translator as an inspection tool, it is always possible to accurately return the stone blocks to their original position to continue processing, if they were moved for some reasons before. Installation of wedging stones between the backsides of the blocks and the ground provides the necessary position fixation of the blocks in space.
The above described process of topography transfer shows that if one provide the carrying rod with the same pointed tips as the measuring rod has, and make the measuring rod as thick as the carrying one, and also provide the measuring rod with the same cylindrical hinges (pos. 14 in Fig. 4(b)) as the carrying rod has, then we get a modification of the translator of symmetrical design, where there is no difference between the carrying and measuring rods. Such translator may be more convenient while moving it over the being processed stone surface of large area, however, it will have a heavier and less sharp probe-pointer.
Above, the conjugation of two adjacent blocks over one section was described. The next section will demonstrate how the polygonal masonry as a whole could be created using the proposed translator.
2.11.3. The sequence of processing by the translator of stone blocks in the polygonal masonry
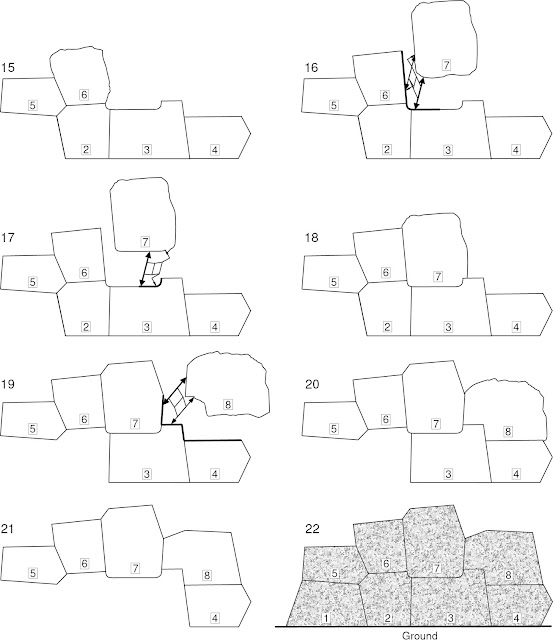
First, the stone blocks forming the first course of masonry are processed. For the first block of the first course, a stone of arbitrary shape is taken (see Fig. 5, pos. 1), in which the side faces (base, top side and lateral sides) are formed (pos. 2). The processing of the side faces is arbitrary – an initial irregular side surface of a natural stone is replaced with a set of the approximately plane faces. Next, these faces will no longer be processed. The block obtained as a result of such processing is put on the ground backside down (pos. 2). Further, the processing, fitting and quality control of interfaces between the adjacent blocks will be carried out for this orientation of the blocks.
For the second block of the first course, the next stone of an arbitrary shape is taken, in which a flat base is fabricated. Then, the block is put next to the first block so that the bases of the blocks are located in the same vertical plane (pos. 3). The translator is installed between the blocks parallel to the bases of these blocks. After that, the topography is transferred from the lateral side of the first block to the lateral side of the second block (the copied area is shown by a bold line).
If the joining lateral sides of the blocks are perpendicular or almost perpendicular to the bases then the translator is installed on the flat supports; otherwise, the translator is installed on the pointed supports. If the joining lateral sides of the blocks are inclined to the bases at too acute angles (less than 45°), then the bent tips are screwed in the measuring rod; otherwise – the straight tips. The translator in Fig. 5 is represented schematically. To avoid detail overloading of the figure, the carrying rod movements over the processed area related to the translator's range exhaustion are not shown hereinafter.
 |
| Fig. 5. Continuation. |
After fabrication of the interface area, the blocks are joined (pos 4). Then, on the remaining side surface of the stone billet of block 2, the rest (arbitrary) faces of this block are formed (pos. 5). As before, the processing of these faces except for the significantly curved areas in L- and U-shaped recesses (pos 7) is flattening of the complex initial shape of a stone billet by surfaces close to planes. The above steps are repeated for the third, fourth (pos. 5-10) and, if necessary, for the subsequent blocks of the first course. Having completed the first course construction, one proceeds fabrication of the second course of the masonry (block 5, pos. 11).
Unlike the blocks of the first course, where the joining of the adjacent stones took place over one side section usually, the blocks of the second and the subsequent courses are joined over more than one section. As a rule, the joining of these blocks is carried out over the base and the lateral side adjacent to the base (pos. 11). If the angle between the sections being copied is close to 180° then the translator is installed on the flat supports. Otherwise, the translator is installed on the pointed supports.
The block to be fitted should be located relative to the masonry so that the translator installed on the pointed supports would be inclined approximately the same to both sections being copied. If the angle between two copied sections is too sharp (less than 45°) then the bent tips are screwed into the measuring rod, otherwise – the straight tips. If the bent tip is unable to penetrate into a too sharp internal corner then such angle should be replaced in the masonry by a rounding of a suitable radius.
Note that the interface sections between the blocks in Fig. 5 are just shown as rectilinear. In practice, all these sections are curvilinear to greater or lesser extent. After processing block 5 and checking quality of its joining (pos. 13), block 1 can be removed from the temporary masonry (pos. 14) and passed to the final assembly of the wall (pos. 22). The processing of block 6 is similar to the processing of block 5 (pos. 14-16).
Processing of block 7 for the U-shaped recess consists of two steps. First, the lateral side of block 6 and an approximately half of the U-shaped recess in the blocks 2 and 3 are copied, which is the first (direct) L-shaped recess (pos. 16). Then, copying of the U-shaped recess continues on the second (counter) L-shaped recess (pos. 17). Copying of the direct L-recess (pos. 16) can be performed by both the straight tips and the bent tips (in Fig. 5, both types of the tips are shown together for clarity). Copying of the counter L-recess (pos. 17) is performed using the bent tips. Note that during transferring the direct and counter L-shaped recesses, the translator orientation in space should remain unchanged.
If the straight tips were initially screwed in the measuring rod while transferring the U-shaped recess then they should be replaced with the bent ones at the second step (the specified distance between the ends of the probe and pointer should remain unchanged). If the bent tips were initially screwed in the measuring rod while transferring the U-shaped recess then at the second step they should be turned by 180° by screwing in the probe and screwing out the pointer (or, vice versa, by screwing out the probe and screwing in the pointer).
In case of a large number of acute angles and U-shaped recesses in the masonry, it is convenient to use the topography translator whose measuring rod has cylindrical hinges providing free rotation of the measuring rod around its own axis (see Fig. 4(b)). The adjustment of position of the bent tips of the measuring rod for operation on the first and second L-shaped recesses is actually reduced to revolution of the measuring rod around its axis by an angle suitable for the given location.
Having installed block 7 at its place (see Fig. 5, pos. 18), the remaining side surface of this block is subjected to the arbitrary processing (pos. 19). Having completed block 7, block 2 can be removed from the temporary masonry (pos. 19) and moved to the polygonal wall construction site for its final installation (pos. 22). If a block of the previous course is unextractable or hardly extractable at the current stage of the block fitting then this block can be extracted later, when the blocks retaining it will be completed.
Fitting of block 8 (pos. 19-21) is clear from the figure. If necessary, the third and subsequent courses of the polygonal masonry are fabricated similarly to the fabrication of the second course of the masonry. The final view of the wall consisting of eight blocks laid in two courses is shown in the figure, pos. 22.
2.11.4. Specifics of the topography translator application
The operation of the proposed device is based on the well-known principle of conjugation of two surfaces.7 In article 11, this principle of conjugation of stone blocks is taken as a basis of the method of polygonal masonry fabrication. In contrast to the method described in article 11, the operation position of the topography translator in space in the method under consideration due to the double parallelogram mechanism can be arbitrary.
In practice, the most convenient positions of the translator are close to horizontal as they allow the stonemason to process vertically located mating surfaces of stone blocks lying on the ground opposite to each other. The front surface of a stone block is located horizontally and is also fully accessible for processing. Moreover, the blocks fitted according to the proposed method can be joined in this position with each other (using wedging stones) that allows us to check the quality of the implemented interfaces before putting the blocks into a wall.
In method 11, due to referencing the measuring rod to the vertical by means of a plumb line, the stonemason in order to process the upper side of the block of the previous course has to put the block of the current course, by which base the fitting is performed, above the block of the previous course that is unsafe and requires a lot of additional efforts. In particular, it is necessary to provide stops (recesses or protrusions) on the stone blocks, fabricate logs-stops, bury these logs-stops into the ground, put the stone blocks on the logs-stops at the beginning of the work, and take down the stone blocks from the logs-stops after finishing the work. Meanwhile, platforms, scaffolds, ramps, etc. are required to access the processed surface from the front side of the wall and to access the front side itself. Moreover, the use of the plumb line in method 11 significantly reduces stonemason productivity as a lot of time is required to calm the plumb line during the surface treatment of the block. In addition, the use of the plumb line itself can be very difficult in the event of a strong wind.
Vincent Lee, the author of article 11, initially proceeded from the fact that the polygonal masonry in the Peruvian megalithic structures was created by the Indians. In accordance with this initial assumption, Vincent Lee was forced to use a plumb line as the simplest measuring tool that could be known to the Indians at that time. Moreover, the author wanted to somehow use in the method he proposed the protrusions (bosses) and recesses on the front sides of the stone blocks of the Sacsayhuaman Fortress for creating the polygonal masonry. Hence, an extremely costly arrangement of the processed stone blocks, one above the other, arose in terms of the applied efforts.
In the proposed method, the parallel movement of the measuring rod is in no way connected with the normal to the Earth's surface and can occur at any orientation of the translator. Therefore, the fitting of the blocks and their pre-assembly are performed when the current and the previous courses of the blocks lie on the ground with their backsides down. Hence, as in the case of the 3D-pantograph application, a sign of using the block fitting method will be the same inclination of the chisel marks on the mating faces of the stone blocks to the direction passing perpendicular (almost perpendicular in the case of a slight wall slope) to the front surface. Only after completing the laying of the blocks of the current course on the ground, the blocks of the previous course can be installed on their positions in the wall under construction. Therefore, in the proposed method, there is no need to process the stones on the wall being erected in the cramped conditions and at the risk of life.
Topography transfer of the adjacent sections with a sharp boundary and with a smooth boundary (for example, in the form of L- or U-shaped recesses) is performed in a single operation. This means that the orientation in space of the carrying/measuring rod and the distance between the probe tip and the pointer tip of the measuring rod remain unchanged at both sections all the time. When passing to the section of the counter L-recess while transferring the U-shaped recesses, it is necessary to replace the straight tips of the measuring rod with the bent ones or to turn by 180° the bent tips, if they were used initially.
During the topography transferring, the translator is often located at angles to the joined surfaces which significantly differ from the normal (see Fig. 5). Such translator orientation in the case of the sufficiently sharp probe and pointer causes just an insignificant additional error of topography transfer. The greater is the deviation from the normal and the larger is the radius of curvature of the probe and pointer tips, the larger is the value of this error. The bent probe and the bent pointer are intended for use in the case when the straight probe is at a small angle to the surface to be copied.
The block fitting method described in the present paper could be used for construction of walls with comparatively simple polygonal masonry, where the mating surface areas have a small curvature, there are no figured cusps or sharp steps at the triple junctions (there is no “feeling of modeling”, see the next section). Since in the method under consideration, the sequential fitting of the blocks “by site” is performed, the sign of this method usage will be the mounting of large blocks in the first course of masonry directly on a strengthened soil or on a pre-prepared bedrock, i. e., without the small “alignment” blocks in the first course of masonry that ensure the correct mutual position of the large blocks of the second and the subsequent courses (see more details in Section 2.1). If we see that, according to all signs, the method of block fitting “by site” was used, but the large masonry blocks lie on small blocks, then this means that the masonry was once reassembled and may have been moved here from another place.
Another sign of the topography translator usage will be the small paired recesses located strictly opposite each other (the larger is the area of the mating surface, the greater is the number of the recesses). The recesses are made at those locations where the carrying rod of the translator is installed on the pointed supports at some angle to the mating surfaces. The presence of a set of low-contrast annular regions superimposed on each other on one of the mated surfaces can also serve as a sign of the use of the proposed above topography translator. One more sign of the translator usage is the presence of a “visor”, which often occurs during the block fitting (see Fig. 5, pos. 4, block 2; pos. 6, block 3; pos. 18, block 7; pos. 20, block 8). Sometimes, such visors are found on incomplete blocks, being, in turn, a sign of the block unfinisheness.27
It should be noted in conclusion that the main advantage of the proposed method is that half of the mating surfaces of the stone blocks are processed arbitrarily.
3. Polygonal masonry peculiarities, questions related to dating and authorship, economical grounds
3.1. A general bulge of the front side and a swell in its lower part, bosses, cusps/steps at the triple junctions, polygonal bas-relief facing
A typical general bulge of the front surface as well as a swell in its lower part (should not be confused with the bosses) found in some structures (see, for instance, Photos. 1-4) often serve as one of the proofs of the “plastic” version13-15 of the polygonal masonry fabrication. According to the plastic version, the partially solidified blocks were stacked one on another. As a result, the interblock gaps in the polygonal masonry were closed under own weights of these blocks and the front surface got the specified bulge and swell.
In the proposed method, both signs – the bulge and the swell can appear by themselves at the stage of fabrication of the clay model of the wall unless the clay mixture was not thick enough and no sheathing was used on the front and back sides. The bulge and the swell can also be produced intentionally while sculpturing the clay model.
Most likely, the bulge and the swell were given to the blocks intentionally. Both features increase the feeling of massiveness, grandiosity of the structure, its colossal weight; it seems to us as if the stones are flattened under a huge weight. The bulge was also intended to demonstrate to the naive Indians the power of the arrived whites, who could “sculpt”, if necessary, a building out of huge hard stones as if from dough.
As for the bosses (see Photo. 9), besides an architectural decoration, they serve as a kind of a signature of the group of the professional builders (see Section 3.5) who created the structures in Peru and similar ones around the world. The bosses whose sizes, shape and location obey no regularity were created from stone blocks of arbitrary shape in cases when there was simply an excess of material of suitable sizes in some place on the side that was supposed to become the front side. In the stone blocks which bosses possess a regularity, to obtain the bosses a layer of material was intentionally removed from the front surface. In the latter case, the bosses usually protrude outside slightly, because the more the boss protrudes, the thicker is the layer of the material that must be removed from the front side.
 |
| Fig. 6. Cusps and steps. |
The cusps (“beaks”) and steps (see Fig. 6) are clearly visible in the points where three adjacent blocks meet. These elements are produced while sculpturing the clay model and then transferred on the stone block with the pantograph. Besides a stop limiting movement of the adjacent block in the horizontal plane, the cusps give the polygonal masonry a special grace. According to the creators’ idea, the cusps along with the parallelism of the smoothly changing curved edges were intended to give a sense of easiness of working with stone. These features make the viewer think that the blocks are literally sculpted of stone. We must pay a tribute to the old masters; they succeeded in this technique!
Given the above, instead of the term “polygonal masonry”, it would be quite fair to use the term “polygonal sculpture” in the cases when a stone structure is created on the basis of hand-sculpting of a clay model made in a certain artistic style with unique lock interfaces between blocks. Besides the simple dressing of the front side of the stone blocks, the proposed technology allows to create a polygonal masonry which face surface is a bas-relief. The temple complex Angkor26 is the example, where such facing technology may have been applied.
3.2. Indirect dating by the observed destructions of the masonry elements
The cusp is one of the weak points of the polygonal masonry in terms of strength. Thus, the cusps should fail first during the natural weathering process. Many stones in Peru are covered with a lichen (see Photos. 7, 9), so the biological factor must also be taken into account in addition to the weathering when estimating the rate of the stone destruction. Surprisingly, the type of the polygonal masonry under consideration is perfectly preserved in the mountains (Cusco, Machu Picchu, Ollantaytambo, etc.), where the climate is characterized by sharp temperature changes 15-20° C during a day, by a lot of precipitation and by light frosts in winter (June-August).28
Besides weathering, a shift of stones in the masonry during an earthquake or during a landslide move of the slope (often triggered by an earthquake) can cause destruction of the cusps.3-5 It should be noted that the cusp cleavages could occur in the process of stone block fabrication, during transportation, installation, or restoration. Some of these cleft cusps can be partially repaired. The repaired cusps will look more sunk into the body of the masonry than the normal ones.
The study of the polygonal masonry from hard rocks (granite, andesite, basalt) shows that the cusp damages are present but they are few in number. The absence of noticeable destructions under fairly harsh climatic conditions and high seismic activity in Peru give a reason to assert the comparatively recent, for about 300 years, construction of the megalithic complexes. A rough estimate can be obtained by comparing the state of the megalithic complexes with monuments being in similar weather-climatic conditions made of similar materials, whose date of construction is known for certain.
3.3. How to prove it? What should we look for and where?
What can serve as a confirmation of the proposed methods of fabrication of the polygonal masonry? On the territory or near the complexes with the polygonal masonry or in quarries, construction debris should remain, in which fragments of clay model blocks and fragments of clay/gypsum replicas should be searched for. Certainly, first of all, we need to study the materials of the conducted excavations. It is not unlikely that some suitable fragments in shape, size, and materials have already been found and documented. Most likely, much of the debris was used for strengthening the ground under the next erecting structure. Therefore, in the case of setting up again any structure damaged by natural causes, the evidences in the form of the clay models and replicas should be sought in the ground under the structure itself.
Assuming that in the pantograph used by the builders, the clay model and the stone billet were positioned in the same way as in the modern pantograph, i. e., horizontally with the backside down (to fix the block in case of uneven back surface, wedging stones are used), then the chisel marks on the side surface of the stone blocks should go from right to left (chisel in the left hand, hammer in the right) and from top to bottom (at the beginning of the trace, the recess is larger than at the end). The marks themselves should be short parallel strokes arranged in vertical columns.
The chisel marks should be searched for on the stone blocks from hard rocks – granite, andesite, basalt. Soft rocks, such as limestone, have a high porosity; the surface layer of these stones is quickly destroyed by weathering. Moreover, the chisel marks on the limestone surface are easily destroyed during the subsequent smoothing operation by tapping. Because of weathering, there is also no sense to study the interface surfaces of the stone blocks from hard rocks that have lain in the open air outside masonry for an unknown number of years. To analyze an interface surface, one should take stones from some untouched masonry having minimal gaps, which could get a very small amount of moisture.
It should be noted that the several hundred years old masonry of stone blocks is most likely impossible to disassemble so as to keep the surface layer of stone intact in the contact areas. The fact is that during the entire period of the masonry existence under the above mentioned climatic conditions, various physico-chemical processes took place in the contact areas causing a change in the mineral composition in these areas. As a result, depending on the process, the contact could break down (with sand formation) in some areas and, on the contrary, strengthened in other areas. An attempt to separate the areas, where the strengthening has occurred, will result in the destruction of the stone surface layer adjacent to the contact. Anyway, the sizes of the stones and their geometry will change after disassembling the old polygonal masonry. Therefore, it is impossible to reassemble the old blocks so that there would be the former tiny gaps between them.
3.4. Indirect dating by the invention time of the 2D‑ and 3D‑pantographs
If we accept the proposed methods of the polygonal masonry fabrication, the structures of “incredibly” ancient Incas can be approximately dated by the years of invention/building of pantographs by Europeans. The pantograph for working with a flat drawing was invented in 1603-1605 by Christoph Scheiner.29 Moreover, the author has published the information about the device design in the form of a separate book30 only 28 years (!) after the invention.
Comparison of the topography translator with a 2D-pantograph shows that these devices are similar in terms of their mechanical complexity, operation accuracy, used materials, and fabrication technology. This implies that the topography translator could well have been invented and built in the early 17th century. The topography translator could have appeared even earlier, since it is functionally simpler – it does not need to solve the problem of proportional scaling.
Around 1710-1720, Russian mechanics Franz Singer and Andrey Nartov31 built a turning machine for copying medals.32,33 The machine was intended for production of medals in automatic mode by transferring a relief from a large size medal model. It is not quite correct to compare the Singer-Nartov machine with the modern 3D-pantograph used by sculptors (see Fig. 2), since the kinematic diagrams of these mechanisms differ greatly. Despite this, attention should be paid to the complexity of the machine mechanism, which notably exceeds the complexity of the modern pantograph mechanism. In particular, the probe movement along the model surface and the cutting tool application to the billet surface in the 3D-pantograph are carried out by the sculptor manually, whereas these functions are implemented in the given example of the machine without a human intervention. Note that copying machines like this were built and used in many European countries in the 18th century.
In 1807, James Watt34 starts designing a mechanism35 intended for production of reduced copies of sculptures.36 The kinematic diagram of the Watt's mechanism is close to the kinematic diagram of the modern 3D-pantograph. However, there are a number of differences. Instead of the ball joint, the boom is mounted on a universal joint; there is no a parallelogram mechanism; the model and its reduced copy are located horizontally, etc. In order to scan the surface of the 3D-object being copied, in the horizontal plane one performed a reciprocating-rotational motion with the pantograph boom relative to the vertical axis of the universal joint.
The kinematic diagram of the pantograph built by Benjamin Cheverton37 in 1826 is the closest to the kinematic diagram of the modern 3D-pantograph (see Fig. 2). Building the pantograph, Cheverton relied on the design previously proposed by John Hawkins.38 Just like the Watt pantograph, the Hawkins-Cheverton pantograph was intended to produce reduced copies of sculptures.
It should be noted that both the Watt pantograph and the Hawkins-Cheverton pantograph had a built-in engraver, whose milling cutter performed mechanical processing of the billet. An engraver is not required in the above considered methods creating the polygonal masonry. Therefore, the construction pantograph is mechanically simpler than the Watt and Hawkins-Cheverton pantographs. The drawing shows a studio of the second half of the 19th century, in which mass copying of statues was carried out manually using a 3D-pantograph.39
 |
| Dwg. 1. A 19th century studio of statues manual copying using a 3D-pantograph (ink, artists E. Morin and E. Rovens, 1864). |
There is no doubt that, having created a 2D-pantograph at the beginning of the 17th century, scientists of that time and, first of all, the inventor of the 2D-pantograph himself, Christoph Scheiner, immediately thought about creating a 3D-pantograph mechanism with which it would be possible to obtain reduced/enlarged copies of three-dimensional objects. Actually, for transition to work with three-dimensional objects, the 2D-pantograph just had to be fixed not in the cylindrical, but in a ball or universal joint, and the model and the billet should have the ability to synchronously rotate around their vertical axes by means of a chain (see Fig. 2) transmission or a gear transmission (see Ref. 37).
Application of the chain transmission in the construction pantograph is more justified in comparison with the gear transmission. The point is that large dimensions and weight of the processing stone blocks result in large dimensions and weight of the used gear wheels. Moreover, the chain transmission makes it easy to change the distance between the rotating platforms, which is responsible for the pantograph reducing/enlarging factor. The distance change is carried out by shifting the platforms along the frame. For this purpose, a corresponding number of links is added to or removed from the chain and/or the chain is pulled by a roller located at the end of a spring-loaded console. In this case, the reducing/enlarging factor turns out to be almost continuous. To change the distance in the case of a gear transmission, the installed set of wheels is replaced with the most suitable one among available sets which number is usually limited. Therefore, the reducing/enlarging factor turns out to be strongly discrete.
Analyzing mechanisms similar to the Singer-Nartov machine, we can conclude that development and building of the modern design 3D-pantograph from the point of view of the kinematic diagram complexity, the metal-working technology, and the used materials were quite feasible for mechanics in the early 18th century already. By that time, all the problems related to the copying accuracy, namely: gaps in the ball and cylindrical bronze joints, backlashes in the chain/gear transmission, as well as the boom and frame rigidity (required the relative position of the pantograph elements stay unchanged during operation), had already been successfully solved. Therefore, it is very strange that it took so long to create a 3D-pantograph, more than 220 years!
Today, we still have neither written nor material evidence confirming the existence of a construction 3D-pantograph in the 18th century. Nevertheless, taking into account the state of the art of those times, one cannot exclude a chance that such a pantograph could have been developed, built and found a limited usage in construction, but the inventor itself and his pantograph had remained unknown to a wide range of experts. The fact is that the master masons in those days were in no hurry to disclose their professional secrets. Judging by how long the mystery of the polygonal masonry creation had persisted, the master masons were able to keep their secrets well.
3.5. Who built this, when and with what funds?
The problem regarding the structures based on the polygonal masonry is as follows. The official history states that the structures had existed before the arrival of Europeans in the New World in the 16th century, and the American Indians did not know neither iron tools nor a wheel and did not have draft animals at that time. From this statement, there is only one conclusion: the structures were built by some older civilization that existed in America before the Indians, meanwhile whose culture of stone working, in general, corresponded to the European construction culture of the 16-17th centuries.
The problem regarding this mythical older civilization is that it left behind no other material evidences of its existence, except for several perfect stone structures. The high-quality polygonal masonry and the structures based on appear instantly (by historical standards) as if from nowhere, and then disappear also instantly into nowhere.18 There are neither previous nor subsequent noticeable development in architecture and technology of these structures. This may happen only when a group of professional builders comes to a certain territory for a short period, say, for 10 years, with their own tools, contrivances and construction techniques.
Transience of the events taken place in the construction industry of those years indicates the high productivity of the strange builders and their construction methods. The contradictions are instantly resolved if the authors of the structures are visiting European builders,40-44 and the time of erection of the structures is transferred from “minus infinity” to the 17-18th centuries. For delivery, moving, and rough processing of the stones, slope strengthening, and other heavy and unskilled work, of course, the local Indian people were driven together by orders of the Indian chiefs subdued/bought by the Spaniards. Thus, in a certain sense, the Peruvian megalithic complexes are the structures built by the Incas too, although not so ancient.
Any large-scale construction is always based on some strong economic foundation. It is difficult to imagine that the megalithic complexes were built for the Indians at the expense of the Spaniards. Of course, these complexes were created at the expense of the Indians and on bones of the Indians. But what could the Indians offer to the Spanish colonizers? The gold and silver that they had were captured in the early years of the conquest and taken to Europe. The Peruvian land was not able to produce much cotton, sugar cane, or grain.
Since the Indians had gold and silver at the beginning of the conquest, it means they took it somewhere. Therefore, the Spaniards organized gold and silver extraction in mines and goldfields.44-47 And to make the work in the mines more fun, the aboriginal priesthood inspired the Indian people with the appearance and grandiosity of the megalithic temples, which were built at the expense of a part of the funds received from the extraction of the precious metals. After few decades, the easily accessible gold and silver deposits were exhausted, and the construction of the megalithic complexes has stopped. By this time, the power of the Spaniards and the Catholic Church had increased somehow “imperceptibly”, and the number of the Indians was greatly reduced in some “incomprehensible” way.46
Poor food and living in shacks did not add health to the miners, the places of “strength” did not longer compensate for the strengths taken away by exhausting work in the mines.46 In general, the time has come when some of the abandoned religious structures of the Indians could finally be put to good use without much trouble. And these structures have been put to good use. Stone blocks and parts of the structures were used for erection of Catholic cathedrals, abbeys, palaces, villas, urban and industrial buildings.
 |
| Photo. 16. A bird's-eye view of the Fortress Sacsayhuaman (www.ollantaytambo.org). Three tiers of the indented bastions and the groundwork remains of a cylindrical citadel are clearly visible. |
3.6. Fortress Sacsayhuaman – the simplest star-shaped fortress
What else does indicate the European authorship of the Peruvian polygonal buildings as well as the time when they were erected? Let us take a close look at the Fortress Sacsayhuaman (Photos. 16, 17). What is this building? Before us is a kind of fortification known as a star fortress.48
Unlike the star fortresses of late construction that survived to our time, the bastions in Sacsayhuaman consist of one face (a long section of the wall) and one flank (a short section of the wall). The chain of these bastions forms an indented (star-shaped) trace.48 The curtain (a straight section of the fortress wall) is either absent at all here, or is a short section being a continuation of the face. The Fortress Sacsayhuaman has three tiers of the indented bastions. Since the faces are not parallel to the front of an advancing enemy, but they are located at a noticeable angle to it, then the concept of the flank while describing this bastion type can be abandoned at all, instead considering the bastion consisting only of faces – the long and short.
 |
| Photo. 17. Arranged in three tiers indented bastions of the Fortress Sacsayhuaman (O. Byelikova, dreamstime.com). |
The reason for the observed trace geometry of the Fortress Sacsayhuaman was the desire of the fortress builders to simplify the retaining wall as much as possible, minimizing the number of kinks per a bastion. Despite this simplification, the possibility of firing at the approaches to the face (and the face itself) of the bastion located on the right, and firing at the approaches to the flank (and the flank itself) of the bastion located on the left remains. Impossibility of the complete cross-firing of the enemy located near the fortress wall between the adjacent bastions or climbing this wall should be considered as a disadvantage of this trace. Nevertheless, the presence of a rifleman in the corner between the bastions makes it possible to fire along both rather short sections of the fortress walls coming out from this corner and, thus, partially ensure the cross-firing ability at these locations.
Unlike a typical star fortress, the chain of the indented bastions of the Sacsayhuaman does not form closed defense rings in its current state at least. Nevertheless, as a star fortress should be, it had a citadel inside. Judging by the groundwork remains, the citadel was a cylindrical tower.
Unlike a typical star fortress, the use of cannons was not envisaged in the Sacsayhuaman. There is simply no place for them in the star rays (bastions). The use of cannons even of a small caliber (there should be at least two for each bastion to cover the face of the bastion on the right and the flank of the bastion on the left) would have required a significant increase of the bastion size. Moreover, the number of the bastions should be significantly less, since the distance between the bastions in the case of use of cannons cannot be so short as in the Sacsayhuaman. Finally, cannons are too powerful weapons against the Indians and other more strong enemy was not expected at that time.
If an enemy overcame the first fortress wall, the fortress defenders in the second defense echelon as well as the joined to them survived defenders from the first echelon opened fire on him. In the case of the second echelon capture, the situation was repeated – the survived defenders of the first and the second fortress walls joined the defenders of the third wall. Each next defense echelon is a chain of the indented bastions located in such fortresses above the previous one forming tiers. In the event of the third echelon surrender, the survived defenders took refuge in the citadel – the last line of fortress defense, and fired the enemy through the embrasures available there.
One of the key parameters of the star trace is the distance between the vertices of the neighboring rays (distance between the ray vertice at the parapet level of a bastion and the ray vertice at the foot level of a neighboring bastion). In the Sacsayhuaman, this distance changes within the range 10-30 meters, it makes about 18 meters on average (the estimate relates to the lower bound as the bastion heights were not taken into account).27 Another important trace parameter is the value of the outward protrusion of the star rays (bastions), that is, how long the rays are. In the Sacsayhuaman, the ray lengths make about 6 meters on average.27 Finally, the third parameter of the fortress, which should be taken into account while analyzing, is the distance between the going parallel fortress walls (actually, stone-faced earthen ramparts). The distance between the first and the second walls makes about 8 meters on average; between the second and the third – about 3 meters on average.27
The presented parameters of the Fortress Sacsayhuaman definitely indicate the weapon that was used for its defense. This weapon must have the aiming range of shooting and the damaging ability at a distance no less than the spacing between the vertices of the adjacent rays. It is not necessary for such weapon to tear bodies apart and scatter them around the surroundings, it is enough to cripple the attacker so that he would no longer be able to climb the wall or to resist actively. In case the fortress defenders retreat to the overlying tier, the used weapons should effectively hit the enemy who had captured the underlying tiers. When sheltered in the citadel, the weapons used by defenders must continue to be effective against the enemy besieging the citadel.
At the same time, in order to be in safety, the weapons of the fortress defenders should exceed the weapons of the attacking Indians – stones, arrows, and spears in terms of the aimed shooting range and deadly force. Note that the Spanish soldiers were equipped in leather and metal armor, which could hardly be penetrated by a bullet fired from a flintlock pistol; most of the Indians did not have any wearable protection. Taking into account that the stones, arrows, and spears had to be thrown upward, i. e., against gravity, the inclined range of aiming throwing among the Indians was about 10-15 meters while preserving a deadly force of their weapons.
Considering the above presented information, a 17-18th century musketoon (known as the blunderbuss in Great Britain or as the trabuco in Spain) – short smoothbore flintlock gun of large caliber (25-29 mm) firing a charge of buckshot, is well suited as the main weapon of the fortress defenders.49 In those days, the musketoon was actively used in cavalry, navy and for fortress siege/defense.49 This type of small arms is designed to destroy large masses of weakly protected enemy at short distances up to 30 meters.
It is worth noting that besides the fire qualities, during a shot the musketoon generated a deafening (thunderous, hence the name blunderbuss) sound, a bright flash of flame and a lot of gunpowder smoke, which together produced an additional frightening effect on the Indians. Also, do not underestimate the overwhelming, formidable appearance of the Sacsayhuaman Fortress itself, which, in combination with the firearms capabilities, inspired fear and awe in the Indians.
To destroy the enemy on distant approaches to the fortress, a musket – flintlock gun with a long rifled barrel, was used. Since to repel an attack successfully, there should be at least two shooters on each indented bastion, the garrison of the Fortress Sacsayhuaman had to be consisted of 42 soldiers at least, considering the number of the available (survived to this day) bastions (the first wall includes 20 bastions, the second – 21, and the third – 18).
During construction of the Sacsayhuaman Fortress, it was assumed that the aboriginal Indians would be the main opponent to the regime established in Peru. In general, the armed resistance of the Indians was suppressed in the early years of the conquest. Nevertheless, uprisings broke out periodically and the risk of a major rebellion remained for many years. Gradually, the Indians completely submitted to the new authorities and then quite peacefully coexisted with the Spanish colonizers.44-47 Thus, after some time, the need for a fortress capable to protect from the Indians but unable to protect against a more serious enemy having guns and cannons in their arsenal fell away. Therefore, the Fortress Sacsayhuaman, which required funds for maintenance, was partly disassembled and over time abandoned.
It should be noted in conclusion that the Fortress Sacsayhuaman in comparison with other Peruvian monuments contains perhaps the largest number of suspicious blocks that have signs of casting, sculpting, or plastering (see details in Sections 1, 2.2, 2.5). Since these blocks do not contain any marks and there is no a chart indicating which of the blocks are original, which replace the missing blocks, or which have been restored, then any of these dubious blocks of the monument should be considered as a fake, deliberately misleading the public about the antiquity of the building and the methods used in its construction.
3.7. Phenomenon of the “tired” stones
So far, a number of questions regarding the phenomenon of the “tired” stones remain unanswered. The tired stones are scattered in a picturesque mess along the road leading from the quarry to the Fortress Ollantaytambo.6,10 How could the tired stones have lain for hundreds of years on a road side (some right on the road) and even in the town limits and not disappear anywhere? The Indians did not worship stone parallelepipeds. Here, if there were, say, niches in these parallelepipeds, then it would be another matter. Meanwhile, to this day, the finally exhausted stones with incredible persistence continue to show us the way to the quarry, where the blocks for the fortress were mined. Why in the mountainous country, where stones are used for the construction of everything – buildings, bridges, roads; these absolutely exhausted stones so conveniently located on the side of the road – take and use, no one has yet been split into smaller parts and put into action? Most of the tired stones are cleft within a day by the efforts of one experienced stonemason. But, instead, we see the complete safety and invulnerability of these stones. It turns out that the local authorities for all these hundreds of years, for some reason, strictly ensured that no one touched these stone blocks.
3.8. Fabrication of symmetrical statues by means of a 3D-pantograph
The casting method, in which, first, a core (solid or hollow) of cheap concrete is cast, and then, after the end of core shrinkage, a comparatively thin shell (“plaster” layer) of more expensive artificial granite is cast over (see Section 2.2), due to its complexity is not suitable for the large-scale polygonal construction, in which all the stone blocks are different. Meanwhile, this method is great both for making single unique statues and for mass production of identical statues.
For example, some “Ancient” Egyptian statues of pharaohs and sphinxes covered with a layer of plaster of artificial stone (granite, dolerite) were apparently fabricated using this technology.24 Since among some “Ancient” Egyptian statues there are statues that differ only in size, it can be assumed that these statues were created by the same original model using the 3D-pantograph adjusted for different enlargement factors.
A number of researchers have long drawn attention to the almost perfect symmetry (face, headdress, torso) of some Egyptian statues (Ramses II, Amenhotep III, Nefertiti).50 The question of how this symmetry was accomplished remained open for a long time. Meanwhile, a small modification of the pantograph mechanism makes it possible to produce statues with a high degree of symmetry of the left and the right sides.24 Let us show how this was achieved in practice.
First, as usual, a sculptor creates an enlarged clay model by the reduced clay model with help of the pantograph. After that, the 0-shaped chain in the pantograph is replaced with an 8-shaped one. As a result of this modification, the platform with the reduced model of the statue and the platform with the enlarged model of the statue will rotate in mutually opposite directions. If the used pantograph has an intermediate gear wheel37 (in the general case, an odd number of identical intermediate gears) to drive the platforms instead of the chain, then a pair of identical intermediate gears (in the general case, an even number of identical intermediate gears) should be installed instead of this wheel or exclude any intermediate gears at all.
Now the sculptor by considering the artistic merits of the left and the right halves of the reduced model of the statue should decide – which side of the statue he wants to exactly copy to its other side. Having decided on the side, let it be the left side for definiteness, the sculptor applies the probe to the left side of the reduced model (the probe must remain perpendicular to the pantograph boom). In this case, the pantograph pointer will show the corresponding point in space on the right side of the enlarged model. If there is an excess of clay at the indicated point, then it is removed directly by the pantograph pointer; if there is a shortage, then the sculptor adds the necessary amount of clay to this point. In order to use the pantograph at probe/pointer angles to the pantograph boom differing from 90° (general case), the parallelogram mechanism should be replaced with an antiparallelogram19 mechanism. To do this, the long bars of the parallelogram just need to be moved into the place of the parallelogram diagonals.
As a result, applying the modified pantograph, it is possible to obtain a sculpture which left and right sides are highly symmetrical. Deviations from symmetry in such sculpture are determined by the error of the pantograph mechanism. To reduce the effect of the pantograph error, the symmetrization work of a head, for example, should start from the nose tip, where the error will be zero, and end at the back of the head, where the error will be the greatest, but least noticeable. Note that a gradual increase in the symmetry violation from the nose to the back of the head will be a sign of the technology based on use of a 3D-pantograph.
There are several polygonal buildings that have short sections of masonry with a symmetrical arrangement of blocks (Sacsayhuaman, Ollantaytambo). However, the symmetry at these sections is only approximate (see, for example, Photo. 11). The blocks on the left and on the right sides of the vertical axis of symmetry are not completely reflection symmetric, they differ in shape and size. Thus, the technical opportunity provided by the 3D-pantograph, that allows to create the polygonal masonry with exactly reflection symmetric sections, was either unknown to the builders of the polygonal complexes at that time or was not simply used.
4. Discussion
Among the materials related to the topic, work 15 should be noted. The author suggested to use a reduced gypsum model of a stone block and to perform transferring and scaling of a complicated surface geometry with a caliper by several reference points. The gypsum model is usually required to avoid wearing of the original clay model while producing copies. This problem does not arise while fabricating blocks for the polygonal masonry. Moreover, in the case of the block model fabrication by a stone billet of arbitrary shape, the clay model is used just once and then thrown out (or serves as a core for a new model). Thus, in order to reach the required result, possessing only a clay model of the block is quite enough.
The transferring process of a complicated surface geometry and its scaling by few reference points using the caliper is very time-consuming and inaccurate. However, this process ceases to be time-consuming and inaccurate if we apply the 3D-pantograph instead of the caliper. Analysis shows that in most cases, first, a reduced clay model is created by a stone billet of an arbitrary shape using the 3D-pantograph. Then, the regions are cut out in the clay model of the block for interfacing with neighboring blocks. After that, a model wall is assembled of the model blocks. After drying, the wall is disassembled, and the interface sites of the model blocks are transferred to their stone billets by means of the 3D-pantograph.
Technically, the topography translator is comparable in terms of complexity to a 2D-pantograph which creation dates back to the beginning of the 17th century. The knowledge accumulated in the field of mechanics and the technology level achieved by the beginning of the 18th century could quite allow to design and build the 3D-pantograph suitable for construction needs. Thus, the most complex polygonal masonry obtained with the 3D-pantograph should be dated to the beginning of the 18th century, and the simpler ones obtained with the topography translator should be dated to the beginning of the 17th century.
The Fortress Sacsayhuaman was built by the Spaniards no earlier than the 17th century, since its very appearance and the defense concept adopted at that time closely related to the small arms available at that moment clearly indicate this. No earlier than the beginning of the 18th century, the polygonal bas-reliefs and the polygonal giant Face Towers of the Cambodian temple complex Angkor as well as a number of the “Ancient” Egyptian giant statues known for their symmetry should be dated, since the 3D-pantograph was needed to create all of these monuments.
Photographs
The photos show the polygonal masonries which can be obtained by using the methods suggested in the article. The distinctive features of these masonries are: the stone blocks are large weighing from several hundred kilograms to several tons, the blocks are mated to each other closely without a gap through complicated curved and extensive surfaces.
Acknowledgments
I thank O. V. Obyedkov, Prof. I. K. Fomenko, O. E. Lyapin, Dr. V. M. Soroka, and D. V. Pisarenko for critical reading of the manuscript and for assistance in conducting this research.
Used materials
2. “List of earthquakes in Peru”, Wikipedia.
3. C. Cuadra, “Dynamic characteristics of Inca’s stone masonry”, ch. 15, pp. 421-460 in book “Masonry construction in active seismic regions” (series in civil and structural engineering), edited by R. Rupakhety, D. Gautam, 466 pp., Woodhead Publishing, 2021.
4. M. A. Rodríguez-Pascua, C. Benavente Escobar, L. Rosell Guevara, C. Grützner, L. Audin, R. Walker, B. García, E. Aguirre, “Did earthquakes strike Machu Picchu?”, Journal of Seismology, vol. 24, pp. 883-895, 2020.
5. K-G. Hinzen, A. Montabert, “Rectangular blocks vs polygonal walls in archaeoseismology”, Annals of Geophysics, vol. 60, no. 4. pp. S0443-0460, 2017.
6. J.-P. Protzen, “Inca quarrying and stonecutting”, Journal of the Society of Architectural Historians, vol. 44, no. 2, pp. 161-182, 1985.
7. E. Laroze, A. Garric, “La technique du sciage des joints dans la maçonnerie ptolémaïque en grès”, Bulletin de l'Institut Français d'Archéologie Orientale (BIFAO), vol. 113, pp. 239-282, 2013 (in French).
8. “Polygonal wall” in Delphi, Greece, Wikipedia.
9. O. J. Outwater, “Building the fortress of Ollantaytambo”, Archaeology, vol. 12, no. 1, pp. 26-32, 1959.
10. J.-P. Protzen, “Inca architecture and construction at Ollantaytambo”, Oxford University Press, 303 pp., New York, Oxford, 1993.
11. V. R. Lee, “The building of Sacsahuaman”, Journal of Andean Archaeology (Ñawpa Pacha), vol. 24, iss. 1, pp. 49-60, 1986.
12. E. M. Shilin, “Polygonal masonry in Peru in South America – a particular view of an architect”, Projects-of-brick-houses.rf (in Russian).
13. Alexander, “Polygonal masonry: cottage technologies”, YouTube, 2015 (in Russian).
14. Alexander, “Polygonal masonry: cottage technologies II”, YouTube, 2016 (in Russian).
15. Unraveling History, “How was the polygonal masonry made?”, YouTube, 2019 (in Russian).
16. Alexander Tamanskiy, “Inca megaliths, polygonal masonry and lie of historians”, YouTube, 2021 (in Russian).
17. “Pantograph”, Wikipedia.
18. GRESAR, “Traces of somebody else's technologies”, parts 1-10, YouTube, 2019-2021 (in Russian).
19. I. I. Artobolevsky, “Mechanisms in modern engineering design: A handbook for engineers, designers and inventors”, vol. 1, Mir, Moscow, 1976.
20. M. Rogińska-Niesłuchowska, “The pantograph and its geometric transformations – a former popular tool for copying and scaling”, The Journal of Polish Society for Geometry and Engineering Graphics, vol. 29, pp. 59-65, 2016.
21. Michael Keropian, “3D Pantograph enlarging”, parts 1-7, YouTube, 2018.
22. Michael Keropian, “Enlarging and reducing sculpture, 3D pantograph”, Michael Keropian Sculpture.
23. “Coefficient of thermal expansion”, Wikipedia.
24. R. V. Lapshin, “How did an unknown sculptor achieve perfect symmetry of the face of the Egyptian pharaoh Ramses II?” (under preparation).
25. SNT chairman, “Who did really build Kronstadt?”, YouTube, 2019 (in Russian).
26. “Angkor”, Wikipedia.
27. J.-P. Protzen, “The fortress of Saqsa Waman: was it ever finished?”, Journal of Andean Archaeology (Ñawpa Pacha), vol. 25, iss. 1, pp. 155-175, 1987.
28. “Climate of Peru”, Wikipedia.
29. “Christoph Scheiner”, Wikipedia.
30. C. Scheiner, “Pantographice seu ars delineandi res quaslibet per parallelogrammum lineare seu cavum, mechanicum, mobile”, 108 pp., Typographia Ludouici Grignani, Rome, 1631 (in Latin).
31. “Andrey K. Nartov”, Wikipedia.
32. “Turning machine for copying medals”, State Hermitage Museum, St Petersburg.
33. V. V. Danilevskiy, “Nartov and his “Clear insight into machines””, edited by A. S. Britkin, 271 pp., Mashgiz, Moscow, Leningrad, 1958 (in Russian).
34. “James Watt”, Wikipedia.
35. “Reducing sculpture copying machine”, Science Museum, London.
36. J. P. Muirhead, “The life of James Watt, with selections from his correspondence”, pp. 454-466, 2nd revised edition, 572 pp., John Murray, London, 1859.
37. “Machine for reproducing sculpture”, Science Museum, London.
38. “John I. Hawkins”, Wikipedia.
39. T. Gauthier, “Photosculpture”, Le Monde illustré, pp. 396-398, December 17, 1864 (in French).
40. Alexander Tamanskiy, “Who and when did build the Egyptian pyramids?”, YouTube, 2020 (in Russian).
41. Alexander Tamanskiy, “How were the Egyptian pyramids built?”, YouTube, 2021 (in Russian).
42. Alexander Tamanskiy, “Who did build the American pyramids?”, YouTube, 2021 (in Russian).
43. Alexander Tamanskiy, “Roman roads of pre-Columbian America”, YouTube, 2021 (in Russian).
44. Alexander Tamanskiy, “American silver in Roman coins”, YouTube, 2021 (in Russian).
45. “Global silver trade from the 16th to 19th centuries”, Wikipedia.
46. P. Bakewell, “Miners of the Red Mountain: Indian labor in Potosí, 1545-1650”, 213 pp., University of New Mexico Press, Albuquerque, 1984.
47. J. J. TePaske, “A new world of gold and silver”, edited by K. W. Brown, 340 pp., Brill, Leiden, Boston, 2010.
48. “Fortification and siegecraft”, The Encyclopædia Britannica. A dictionary of arts, sciences, literature and general information, vol. X, p. 686, fig. 15, 11th edition, University Press, New York, 1910.
49. L. K. Makovskaya, “Hand firearms of the Russian Army from the end of the 14th to the 18th century”, 219 pp., Voenizdat, Moscow, 1992 (in Russian).
50. C. Dunn, “Lost technologies of ancient Egypt: advanced engineering in the temples of the pharaohs”, 400 pp., Bear & Company, 2010.


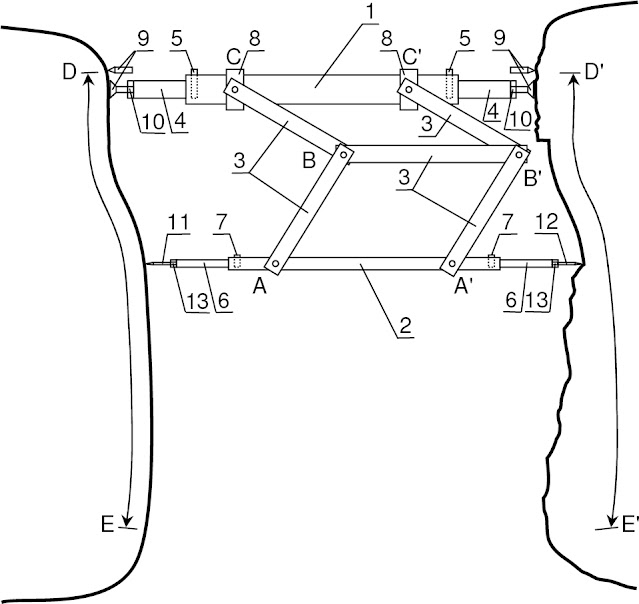


I spent several years in Cusco. My metallurgical background made me note that in Sacsaywaman and other Limestone buildings there were in the junctures an surfaces of the blocks traces of green Copper Carbonate (artificial Malachite) that were not of geological origen. From my experience, If one dissolves Copper Sulfate in water and adds common salt; Copper Chloride CuCl2 is formed as well as innocuous Sodium Sulfate. If Limestone, a natural Calcium Carbonate is added...Copper Carbonate precipitates and very soluble Calcium Chloride. I took some some; disperse rock samples of the place, made a solution and impregnated a fiber rope in a wooden arch a proceeded to "Chemically" saw the rock and it worked in a very precise way. The Malachite is a powder that can be easily washed with the Calcium Chloride. The solution can be also used to polish the Limestone (as can be seen in the boulders faces) Most of Cusco Region Inka constructions are made with Limestone from the extensive Karst geological abundance. Also Copper sulfate is very abundant from the mines there. Mistery? No! It is ancient knowledge. pedroflecha@yahoo.com
ReplyDelete